After reading through a number of issues of Plumbing Connection magazine I felt that while most of the articles are very well written and interesting, some of the content and theory may be a bit challenging for readers without formal hydraulic or engineering qualifications to understand.

To be honest, some of it is challenging for me, and I teach university-level hydraulics. So I thought it might be good to write a series of articles that help explain some of the fundamental fluid mechanics principles in simple, easy to understand terms, for readers who are not engineers.

With that, I thank Plumbing Connection for the opportunity.

What is pressure?

The classical definition of pressure is: “Force per unit Area,” but what does that really mean? Force is measured in Newtons (N), or multiples of N like kilonewtons (kN) which are thousands of Newtons, or Meganewtons (MN) which are millions of Newtons.

The definition of a Newton is a bit complicated to explain but basically has to do with an object’s Mass, and its Acceleration. The Mass of an object is wholly dependent on the number of atoms (or molecules) the object has and this is constant (unless you change the object in some way).

The unit for Mass is the kilogram (kg). Acceleration generally refers to the gravitational forces acting on the object. On Earth, all objects are subjected to the Earth’s gravity force (this is about 9.8m/s2), which is why they have a Weight.

Please note: an object’s Mass is not the same as its Weight. For example, the Mass of an object is the same on the Earth, or on the Moon, or in deep space – it doesn’t change. However, the object’s Weight is very different if it is on Earth, or on the Moon (about 1/6th of the earth weight), or in space (zero Weight).

So for our purposes, a Force can be thought of as the Weight of a stationary object on Earth. Moving objects can also generate other forces but we will discuss that at another time.

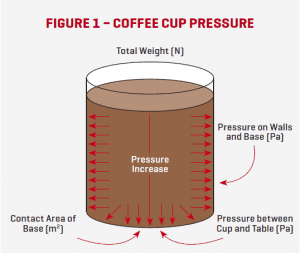
Let’s get back to pressure… If you place an empty coffee cup on the table, there is a certain Pressure created between the bottom of the cup and the table (Fig. 1). The magnitude of the Pressure depends on the Weight of the cup and on the Area of the cup’s base.

The unit of Pressure is the Pascal (Pa). This is defined and the number of Newton’s (Weight force) divided by the number of square metres (Area). If you filled the coffee cup up with coffee, the cup’s Weight (N) would increase, which means the Pressure (Pa) between the cup’s base and the table would also increase.

Pressure is also measured in multiples of Pascals like kilopascals (kPa) and Megapascals (MPa). For fluid systems we usually measure Pressure in kPa, while for construction materials (concrete and steel) we generally measure pressure in MPa. Great, so what’s a coffee cup got to do with fluid or pipe pressures?

Let’s have a look… Now that we have filled the cup with coffee, there are also (static) Pressure forces acting inside the cup on the walls and the base due to the Weight of the coffee (Fig. 1). This Pressure increases as the depth increases due to the Weight of the fluid (coffee) above.

This is a fundamental concept of Fluid Mechanics (for liquids): “The pressure at a particular point below the surface is directly proportional to the height of the liquid above the point.” This means that the static Pressure in a liquid is caused by the Weight of the fluid atoms (or molecules) above it.

Different fluids contain different molecules so they can have different Weights and densities. Density is defined as the weight of a fluid per unit volume. The unit of Density is kilograms per cubic meter (kg/m3). The symbol for Density is the Greek symbol, ư, (pronounced rho).  Fresh water has a density of approximately 1000kg/m3. Oil generally has a density of around 900kg/m3 which is why oil fl oats on water. Concrete has a density of around 2400kg/m3 which is why it sinks in water. Salt water is slightly more dense than fresh water at around ư = 1030kg/m3.

This is why it is a bit easier for us to swim in salt water than fresh water. You may have seen photos of people floating around on the Dead Sea. This is because it has a very high salt concentration with a density of 1240kg/m3. Humans have an average density of around 985kg/m3, so we can easily float on the Dead Sea.

When dealing with fluids, we normally like the answer to Eqn. 1 to be expressed in kPa. To do this, we simply divide the answer by 1000.

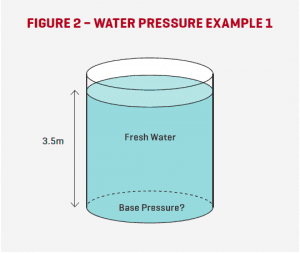
Here is an example to illustrate: Example 1: What is the water pressure (kPa) acting on the internal base of the tank shown in Figure 2? Solution using Eqn 1: P = ưgH = 1,000kg/m3 x 9.8m/s2 x 3.5m = 34,300Pa However, the question asks for the Pressure in kPa, so we simply divide this answer by 1000, i.e.  34,300/1000 = 34.3.  So the pressure acting on the base of the tank is 34.3kPa (answer).

This process is always the same regardless of the liquid being used. The main thing to remember is to make sure you are using the correct Density for the liquid in question. For example, if the fl uid in example one was Oil (ư = 900kg/m3), the base pressure would be approximately 30.9kPa (check this for yourself!).

One of the most important concepts to understand regarding static liquid pressures is that the pressure at a certain point below the surface is only influenced by the height (H) of the liquid above it. It makes absolutely no difference what shape the fluid above or beside the point is.

For example, the water pressure acting on the inside wall of a massive dam 50m below the surface is exactly the same as the water pressure acting on the walls of a Ø5mm diameter vertical tube, 50m below the water surface. However, in this case the pressure would probably be too great for the tube which may cause it to explode.

Many pipes are pressure rated to indicate the strength of the pipe walls. A common classification system is the PN (Nominal Pressure) rating system. It is pretty simple really; a pipe with a PN4 classification can safely withstand an internal fluid pressure of 400kPa. A PN6 pipe can withstand 600kPa and a PN12 pipe can withstand 1200kPa, etc…

For convenience, many fluid system pressures are referred to in metres Head (of the fluid in question). This is really as simple as it sounds. For example, 25m Head of water is the pressure that would be acting on the base of the tank in Figure 2 if the water level was 25m, instead of 3.5m as shown. Water pressure expressed in kPa can be approximately converted to metres head of fluid by simply dividing the kPa value by 10.

For example, a standpipe rated at 250kPa is approximately equal to 25m head of water. However, please note that this conversion will not work for fluids with densities significantly different from water. For example, a pipeline carrying kerosene (ư = 810kg/m3) at a pressure of 270kPa, would be equal to 34m head of kerosene.

Luckily, most of us are generally dealing with water, so this quick conversion method can be useful to remember. Pumps are also generally rated by the amount of Head they produce. For example, a pump rated at 15m Head means it can generate a maximum Pressure of about 150kPa (of water).

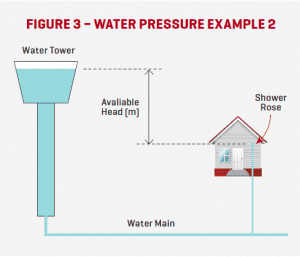
A good understanding of working pressures in water supply mains is important for plumbers as it significantly affects flowrates through pipes and fixtures. Mains water is often supplied by water towers and the water pressure at a dwelling is often governed by the height of the tower above the dwelling and the proximity of the dwelling to the tower, as well as a variety of other variables.

For example, the maximum (theoretical) water Pressure available at the shower rose shown in Figure 3 is the difference in Head between the water level in the tower and the shower rose on the second floor of the house. I say maximum theoretical pressure because there are a number of other factors that will cause pressure losses such as pipe friction and form losses.

However, we will discuss these in more detail in future issues.  Where the available Pressure in a system is too low for the operational requirements, it is common to install some type of pump to increase the system pressure.

If the system pressure is too high, Pressure reduction valves can be used. You may have also heard the term “Bar” used to describe Pressure. One Bar is equal to 100kPa which is approximately equal to the atmospheric pressure on Earth at sea level (101.3kPa). Atmospheric pressure (abbreviated ATM) is caused by the Weight of the air above the Earth.

Although air is a gas which contains lots of molecules flying around, it also has a Density (ư = 1.23kg/m3), and therefore it also has Weight. The Density (and Weight) of air is greatest at the Earth’s surface. Air Density decreases as elevation increases. This is because the further away from the Earth the air molecules are, the less they are affected by gravity. Most of the Earth’s air is contained in the troposphere which is about 12km high.

In addition, the Pressure at a depth of 10m under fresh water is also about 1 bar. So the Pressure at 90m below the water surface is about 9 Bar, etc… This is probably a good time to explain the two terms “Absolute Pressure” and “Gauge Pressure.” Absolute Pressure is referenced against an absolute vacuum. For example, in the atmospheric air pressure explanation above, if you left the Earth’s atmosphere and went into space, there would be no more air molecules so there would be zero Pressure (absolute vacuum).

Gauge Pressure is referenced against atmospheric pressure (i.e. 1 ATM). For example, when you check the pressure in your car tires, the pressure shown is the amount of extra pressure above 1 ATM. Therefore it is also possible to have negative Gauge Pressures (i.e. below atmospheric) under vacuum or siphonic conditions. However, it is not possible to have a negative absolute pressure as this is physically impossible (i.e. you can’t have negative numbers of molecules).

Generally when we are talking about Pressures, we are talking about Gauge Pressures. I hope this article has helped clarified some of the fundamental principles of Pressure for you. In the next article, I will clarify some of the fundamental principals regarding friction and form losses and why they cause pressure drops in fluid systems.

Please feel free to email me any comments, questions or suggestions at tlucke@usc.edu.au.